The story so far
Modern geophysical systems are dominated by coherent structures: jets, eddies, fronts, filaments, and sharp interfaces. In such systems, forecast errors are rarely pointwise or purely additive. Instead, they are primarily structural and geometric, arising from uncertainties in the position, shape, and evolution of these coherent features.
Classical variational data assimilation and recent neural approaches (including 4DVarNet) have demonstrated strong performance in deterministic state reconstruction. However, they typically produce a single optimal trajectory, providing limited insight into uncertainty, especially uncertainty driven by displacement and phase errors.
At the same time, ensemble-based methods often rely on simplistic perturbation strategies (e.g. additive Gaussian noise) that fail to consider non-gaussian error structures such as alignment or positional errors. Such perturbations distort coherent structures, inject unphysical small-scale energy, and poorly represent the dominant error subspaces of advective systems.
This project is motivated by a simple but fundamental observation: In geophysical fluids, uncertainty propagates primarily through large-scale displacements of coherent structures, while small-scale features are advected and deformed by those displacements.
Uncertanty quantification using spatiotemporal random displacements
We introduce an uncertainty model based on spatiotemporally correlated random displacement fields, inspired by stochastic fluid dynamics and Lagrangian flow theory.
Instead of perturbing state variables directly, we model uncertainty through a stochastic flow of diffeomorphisms that acts on the state via transport. These random flows:
- Are smooth and large-scale, targeting the dominant coherent structures
- Are temporally correlated, reflecting finite predictability horizons
- Preserve the geometric integrity of advected fields
- Induce realistic small-scale variability through shear and deformation
Formally, uncertainty is represented by a stochastic displacement field whose statistics are controlled in both space (scale-selective spectra) and time (Ornstein–Uhlenbeck dynamics). This construction allows us to explicitly separate:
Large-scale position uncertainty (phase errors)
Small-scale residual variability (amplitude errors)
4DVarNet-LU: An ensemble neural data assimilation model
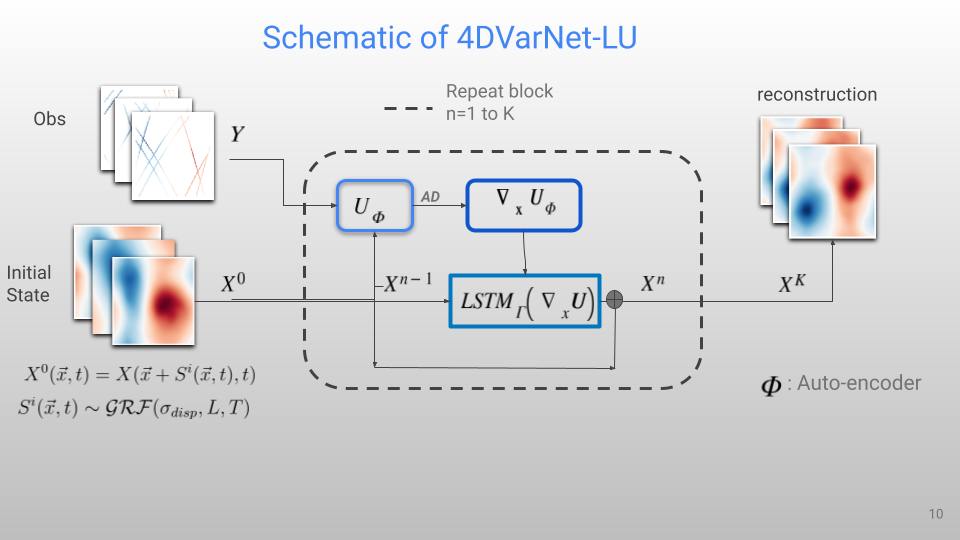
Building on this uncertainty framework, we introduce 4DVarNet-LU, an ensemble extension of 4DVarNet designed to handle Lagrangian uncertainty (LU).
In 4DVarNet-LU:
- Each ensemble member is generated by applying a stochastic displacement flow to the initial state
- All ensemble members are then assimilated using a shared neural variational architecture
- The ensemble is flow-dependent, structured, and physically meaningful by construction.
4DVarNet-LU embeds uncertainty within the architecture itself during generation of initial state, allowing the neural solver to generate multiple reconstructions states.
So what does the 4DVarNet-LU model predicts?
The 4DVarNet-LU model can predicts an ensemble of reconstructed state trajectories, not a single deterministic solution, given a sequence of observations over an assimilation window. This makes 4DVarNet-LU particularly well-suited for applications involving coherent advective structures, where positional uncertainty dominates the amplitude uncertainty.
References
-
Fablet, R., Drumetz, L., Rousseau, F. (2021). Learning variational data assimilation models and solvers. Journal of Advances in Modeling Earth Systems.
-
Beauchamp, M., Fablet, R., et al. (2023). Neural variational data assimilation with learned dynamical priors.
-
Beck, A., et al. (2009). Morphing ensemble Kalman filters. Tellus A.
-
Lawson, W. G., Hansen, J. A. (2005). Implications of stochastic and deterministic filters. Monthly Weather Review.
-
Holm, D. D. (2015). Variational principles for stochastic fluid dynamics. Proceedings of the Royal Society A.
-
Vallis, G. K. (2017). Atmospheric and Oceanic Fluid Dynamics. Cambridge University Press.